Wat enorm helpt is een goede rekenmethode. Die zijn een tijd lang schaars geweest. En met goed bedoel ik: goed gestructureerd, een methode die kinderen leren werken met de eigenschappen van het stelsel. Veel oefenen met het aanleren van de rekenbasis. Wat je hier ziet is de telrol die Rob, mijn man, op de kleuterschool heeft volgeschreven met getallen.
Lezing van Marisca gehouden voor ‘Lezing voor het steunpunt taal en rekenen’ op ….
De rekenrol van Rob

Mijn man Rob Milikowski en ik doen al vele jaren diagnostisch onderzoek. De teller staat inmiddels op 250 (dd. januari 2014). Ik heb een boek geschreven over Dyscalculie en Rekenproblemen en binnenkort verschijnt de NDS, de dyscalculietest die ik samen met onze collega Stephan Vermeire heb gemaakt. Beide worden uitgegeven door Boom. Ik ga u nu kort iets vertellen over dyscalculie.
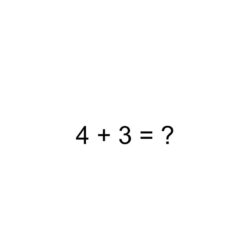
Deze som, 4 + 3 = kun je op verschillende manieren oplossen. • De eerste manier is: alles uittellen. Eerst tel je die 4 uit (doen, 1,2,3,4) dan tel je de drie uit (doen, 1,2,3). Zo. Daar staat de som, op de handen. Nu zien wat de uitkomst is: alle opgestoken vingers tellen. 1,2,3,4,5,6,7. Zeven juf! Heel goed. Kan ook met blokjes, maar vingers zijn wel zo handig. Ik zou dat zeker niet verbieden. Dit is de kleutermanier. Maar in het sbo zag ik de 7-jarige Yassin zo bezig. Elk getal moest eerst worden uitgeteld, anders had hij geen vat op de betekenis ervan. • De volgende stap is om de 4 als uitgangspunt te nemen. Juist, denkt de leerling, ik weet nu wel wat 4 is. En ik ga daar 3 bij optellen. Drie doortellen vanaf 4: 5, 6, 7. Dat gaat al een stuk vlotter.

En dan komt het moment waarop het kind het antwoord WEET. Als je vraagt: hoe heb je dat uitgerekend zegt hij of zij: ik heb niet gerekend, ik wist het gewoon. En dat is waar. Er hoeft niet meer gerekend te worden omdat alle informatie nu op zijn plaats ligt in het geheugen. 4 + 3 = kan niet anders dan 7 zijn, want 7 kun je splitsen en 4 en 3. Is dit kind plotseling begiftigd met een nieuw soort logica? Zo zou ik dat niet willen zeggen. Er is kennis gerijpt in dat hoofd en die kennis heeft een logische structuur. Als mensen rekenen leren zij van steeds meer getallen de belangrijkste eigenschappen kennen. Die bekende getallen raken via die eigenschappen verbonden met andere getallen. Daarom is leren van de tafels zo belangrijk. Die tafelgetallen ontwikkelen zich tot steunpunten in het kennisnetwerk. Neem 12: dat is 3 x 4, dat is ook 2 x 6. Zo krijgt je een systeem in je hoofd.

De omvang van dat netwerk dat mensen er op na houden varieert. Het hoofdrekenwonder Wim Klein, beroemd in de tijd toen er nog geen computers en rekenmachines waren, zei het zo: “Getallen zijn mijn vrienden. Voor u betekent 3844 misschien niet zoveel. Gewoon een 3, een 8, en twee vieren. Maar ik zeg meteen: hallo, 62 kwadraat!” Zijn bestand aan getalskennis was enorm. Dat vormde de basis voor zijn hoofdrekenkunsten.

Het doorsnee netwerk is veel kleiner, maar erg handig in het dagelijkse gebruik. Ik heb in het verleden onderzoek gedaan naar de verankering – in een geheugen netwerk – van de getallen tot 100. Ik legde iemand een getal voor en vroeg hem of haar om zoveel mogelijk getallen te noemen die met dat getal te maken hadden. Zo zag je patronen ontstaan. Bij 9 noemen mensen dan bijvoorbeeld: 3, 10, 18, 81, 90. Je weet dan: hij heeft de 9 goed in beeld. Hij noemt een deler (de wortel), de volgende in de telrij, het dubbele, het kwadraat, het tienvoud. Een mooi netwerkje rond die 9 dus. Die 9 is zo stevig ingebed. Die kan niet makkelijk van zijn plaats. Bovendien wordt zo het verschil met buurgetallen, zoals 8,veel duidelijker.

Kijk: 8 en 9 mogen dan als hoeveelheid nogal op elkaar lijken, hun netwerken zijn totaal verschillend. 8: 4, 8, 16, 64, 80. Hoeveel lijkt dat nog op 9: 3, 10, 18, 81, 90? Weinig. Ook de kleine getallen worden dus door die inbedding beter onderscheidbaar. —

Het probleem bij leerlingen met dyscalculie is dat zulke kennisbouwsel niet ontstaan. Of in elk geval: onvoldoende. 9 is dan een minimaal concept: een halte in de telrij. Of: een datum. Of een leeftijd. Maar niet het kwadraat van 3. Of de wortel uit 81. Te weinig nuttige erkenverbindingen. Dat heeft gevolgen. – Er zijn weinig steunpunten in het rekenen. Weinig steun voor tussen stappen. Handig rekenen is er niet bij. – Tellend rekenen is vaak de enige oplossing. En dat is vermoeiend, aandacht vretend en foutengevoelig.

Kinderen verschillen in aangeboren getalvaardigheid. Bij de een gaat het er in als koek, de ander snap er langdurig niks van. Het gekke is, ook intelligente kinderen kunnen soms merkwaardig veel moeite hebben met getallen en sommen. Ook kinderen met een overigens goed geheugen lukt het soms niet om de tafels te onthouden. Algemene capaciteiten zijn erg belangrijk. Maar gevoel voor getallen is toch een ding apart. Een goede individuele ondersteuning maakt gebruik van de sterke kanten van dit kind; en zorgt ervoor dat de zwakten worden gestut, of ontzien. Vaak loont het om bij problemen al vroeg een degelijk onderzoek naar de cognitieve infrastructuur van een leerling te doen. Hoe zit het intelligentieprofiel in elkaar? Hoe sterk is het auditieve geheugen? Heeft zij steun of juist hinder van visuele hupmiddelen?

Wat enorm helpt is een goede rekenmethode. Die zijn een tijd lang schaars geweest. En met goed bedoel ik: goed gestructureerd, een methode die kinderen leren werken met de eigenschappen van het stelsel. Veel oefenen met het aanleren van de rekenbasis. Wat je hier ziet is de telrol die Rob, mijn man, op de kleuterschool heeft volgeschreven met getallen. Hij zat op de Tweede Montessorischool in Amsterdam, nu het Winterkoninkje, en leerde daar niet alleen goed tellen, maar ook het systeem van notatie. Dat is een prachtig systeem. Met 10 verschillende tekens kunnen we tot oneindig tellen, en daar was Rob hard naar op weg.


Af en toe moest juf Jorritsma hem helpen om een extra strook aan te plakken. —
En dan telde hij door, op weg naar oneindig. Dat was 65 jaar geleden. In de periode na de oorlog kregen kinderen heel degelijk gestructureerd rekenles. Vanaf de jaren zeventig is daar de klad in gekomen. We hebben een heel onordelijke rekentijd achter de rug. Iedereen moest alles op z’n eigen manier uitvinden. Zonde hoor, als er zo’n mooi systeem klaarligt dat je kan trainen om het werk voor je te doen! Twee emmertjes water halen is leuk, om te voelen hoe zwaar die emmers zijn. Maar voor duizend emmers kun je beter de lopende band aanzetten. Dat inzicht is nu weer snel aan het groeien.

Goed rekenonderwijs helpt een stevige fundering leggen. Maar hoe je het ook wendt of keert, ALTIJD zullen er kinderen zijn bij wie het automatiseren van de eenvoudige rekenkennis niet wil lukken. Altijd zullen er kinderen zijn die 4 + 3 stiekem nog even op hun vingers moeten natellen – omdat ze van de uitkomst nooit zeker zijn. Dat probleem heeft lang onder tafel verstopt gezeten. Leerkrachten snapten niet hoe het mogelijk was. Kinderen schaamden zich voor hun domheid.

Nu met de erkenning van dyscalculie hoeft dat niet meer. Het probleem mag open op tafel komen. We gaan dit kind helpen. Met als doel: Het rekenen weer op gang te brengen – De rekenontwikkeling te ondersteunen – En de schoolloopbaan veilig te stellen, zo goed als dat maar kan.
Dank u voor uw aandacht.


